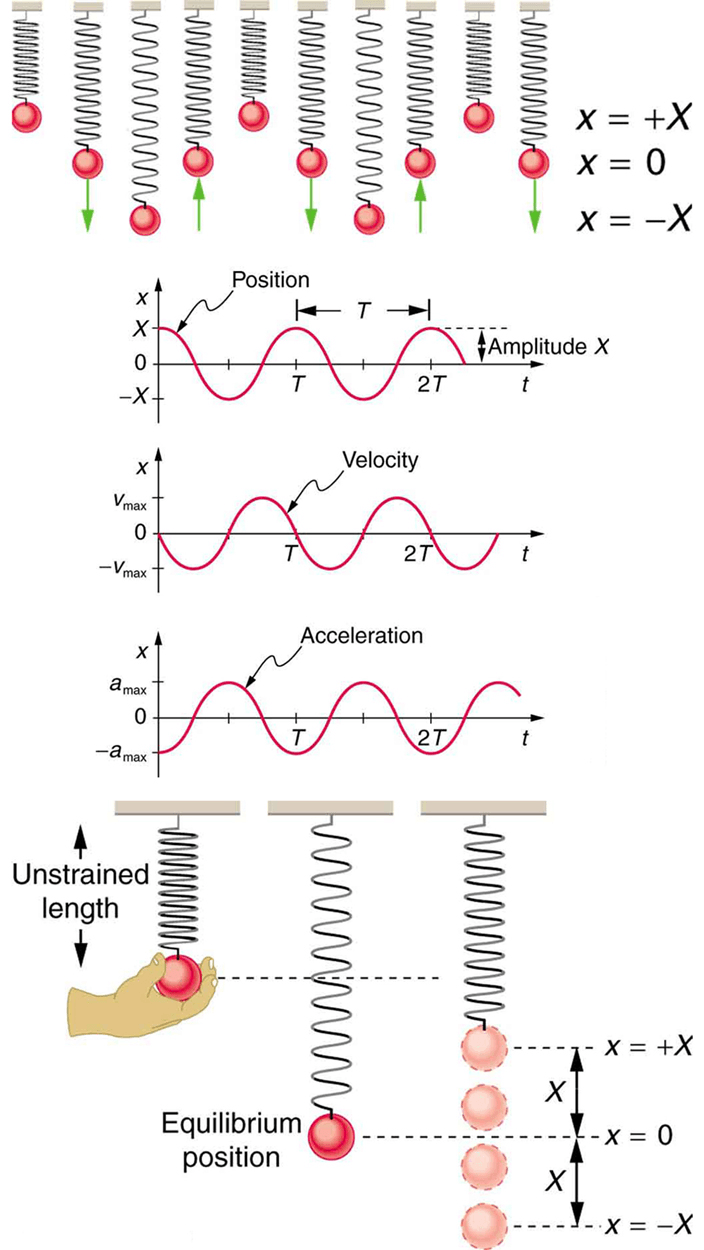
This negative sign means the direction of force is inwards, which can be neglected. So the A cancels out, giving k = -4Mπ^2/T^2. And k = Force divide by displacement, giving k = maximum force divide by the simultaneous maximum displacement, which gives k = (-A4Mπ^2/T^2)/A.Ħ. Simple harmonic motion in spring-mass systems. Level up on the above skills and collect up to 160 Mastery points Start quiz. Suppose a function of time has the form of a sine wave function, y(t)A sin (2 pi t / T) nonumber where (A>0) is the amplitude (maximum value). Simple harmonic motion: Finding speed, velocity, and displacement from graphs Get 3 of 4 questions to level up Quiz 1. So we can get maximum acceleration = -A4π^2/T^2. One of the most important examples of periodic motion is simple harmonic motion (SHM), in which some physical quantity varies sinusoidally. Since we know the amplitude, and we also know the maximum displacement is at t = T/4, which is at Bt = π/2, which is when sin(Bt) = 1, simultaneously having the greatest acceleration of this oscillating system.ĥ. Deriving once will give (A2π/T)sin(2πt/T), which is the function of velocity.ģ. Giving the Asin(Bt) equation as (Amplitude)sin(2πt/T)Ģ. I actually derived the formula of k = 4π^2m/T^2 by differentiating the sin(t) function of displacement twice to find the acceleration, then multiply by mass and divide by amplitude to find spring constant.įirst by finding the specific sin(t) function in the form of Asin(Bt), through the given amplitude(A) and period(T).ġ.